Published on

Facebook Prophet 预测商品价格

Authors
  • avatar
    Name
    Shoukai Huang
    Twitter

Facebook Prophet 预测商品价格

2017 年，Facebook 的一些研究人员发表了一篇名为《Forecasting at scale》的论文，其中介绍了 Facebook Prophet 开源项目，为世界各地的数据分析师和数据科学家提供快速、强大且易于访问的时间序列建模。

1. 基础研究

1.1 背景知识

了解这个技术概念或框架的背景，它是为了解决什么问题而诞生的。

1.2核心概念

Prophet

Prophet 是一个基于加法模型预测时间序列数据的程序，其中非线性趋势与每年、每周和每日的季节性以及假期影响相匹配。它最适合具有强烈季节性影响的时间序列和多个季节的历史数据。 Prophet 对于缺失数据和趋势变化具有鲁棒性，并且通常能够很好地处理异常值。

Prophet is a procedure for forecasting time series data based on an additive model where non-linear trends are fit with yearly, weekly, and daily seasonality, plus holiday effects. It works best with time series that have strong seasonal effects and several seasons of historical data. Prophet is robust to missing data and shifts in the trend, and typically handles outliers well.

2. 理论学习

2.1 Prophet 核心概念

模型定义

Prophet 模型背后的数学方程定义为：

y(t) = g(t) + s(t) + h(t) + e(t)

这是对时间序列的非周期性变化进行建模的趋势函数，s(t)代表周期性的变化（e.g.，每周和每年的季节性），h(t)代表假期的影响，这在一个或更多的日子上可能在一个或更多的天数上发生。错误术语 e(t) 表示模型未适应的任何特殊变化；稍后，我们将做出e(t)正态分布的参数假设。

  • g(t)：趋势函数，用于模拟时间序列值的非周期性变化。用分段线性函数或者logistic函数拟合。 Prophet 使用分段线性模型进行趋势预测。
  • s(t) ：表示周期性变化（例如，每周和每年的季节性），用傅里叶级数拟合。
  • h(t) ：代表在一天或几天内可能出现的不规则日程上的假日影响，用线性函数拟合。
  • e(t) ：误差项。表示模型不适应的任何特殊变化，通常假设其服从正态分布。

详细介绍 Prophet 各个部分的数学原理。 

g(t)：趋势（Trend）模型

Prophet 提供了两种趋势模型：

  • 线性趋势（Linear Trend）：线性趋势用于建模随时间呈现线性变化的情况。Prophet 会在历史数据中自动识别变化点，即趋势突然发生变化的时间点。在这些变化点，模型中的斜率 会进行调整，以适应新的增长趋势。
  • logistic（逻辑）增长趋势：用于建模增长有上限的情况（如市场饱和）。Logistic 模型特别适合那些增长一开始很快，但最终趋向于稳定或饱和的数据场景，比如市场中的产品销售，随着时间推移，增长会逐渐减慢。

s(t)：季节性（Seasonality）模型

由于其代表的人类行为，商业时间序列通常具有多周期的季节性。例如，为期5天的工作周可以在每周重复的时间序列上产生影响，而假期时间表和学校休息时间可以产生每年重复的影响。要适应和预测这些效果，我们必须指定t的周期性功能的季节性模型。

季节性函数 s(t) 负责捕捉周期性波动，比如销售额的周末效应或每年的季节性波动。Prophet 使用傅里叶级数来近似表达季节性变化

h(t)：假期效应（Holiday Effects）

假期和事件为许多业务时间序列提供了大的，有点可预测的冲击，并且通常不会遵循周期性的模式，因此他们的效果无法通过平稳的周期来很好地建模。例如，美国的感恩节发生在11月的第四个星期四。超级碗是美国最大的电视赛事之一，发生在1月或2月的一个星期日，很难以编程方式宣布。世界上许多国家都有主要的假期，遵循月历。特定假期对时间序列的影响通常年复一年，因此将其纳入预测很重要。

假期效应 h(t) 模型用来处理特定日期或时间段对时间序列的短期影响。它使用一个指示函数来表示某些假期或特殊事件

e(t)：误差项（Residual/Error）

误差项，表示模型和实际数据之间的差异。通常假设误差服从正态分布。

2.2 Prophet 适用范围

适用于以下场景：

  • 具有明显季节性和周期性的数据。例如：电商网站的月度销售额，每年“双十一”和“618”期间销量会大幅增长。
  • 存在节假日或特殊事件影响的数据。例如：电力消耗在节假日（如春节）期间会显著下降。
  • 数据存在趋势变化（线性或非线性）的场景。例如：某产品的市场占有率逐年增长，但增长速度逐渐放缓。
  • 数据存在缺失值或异常值的情况。例如：传感器数据在某些时段丢失记录，但需要进行预测。

Prophet 最适合的场景是具有明显季节性、节假日效应和趋势变化的单变量时间序列预测任务，尤其在数据存在缺失或异常值时表现良好。然而，对于高频数据或复杂的非线性模式，Prophet 可能不如其他模型（如 LSTM 或 ARIMA）效果好

2.3 Prophet 预测过程

拟合好模型之后，Prophet 用这个模型来进行未来的预测。预测的步骤是：

  1. 对未来的时间点使用拟合好的 g(t)（趋势），估计它的趋势值。
  2. 使用 s(t) 来计算未来时间点的季节性波动。
  3. 如果未来时间点有假期效应，则考虑 h(t) 的影响。
  4. 最终的预测值为这几个部分的加总，即 y(t) = g(t) + s(t) + h(t)，再加上噪声 e(t)。

Prophet 可以非常灵活地处理各种复杂的时间序列数据。

3. 实践操作

为了更加直观的应用 Prophet 进行数据预测，选取了日常经常购买的商品价格进行价格预测。

最近咖啡喝完了，想继续补充 UCC 117 咖啡作为口粮，到比价网张上获取价格数据。例如：https://www.manmanbuy.com/

通过 Chrome 的网络信息，得到网页呈现价格趋势变化的规格化数据，然后编写算法进行预测。

3.1 环境搭建

安装 Prophet

# 使用 pip 安装
python -m pip install prophet

# 或者使用 conda 安装
conda install -c conda-forge prophet

基本依赖

- Python 3.7+
- pystan
- pandas
- matplotlib (可视化)
- numpy

安装依赖

pip install matplotlib pandas numpy scipy

3.2 示例验证

（1）数据来源

从比价网站上获取商品价格，查看了商品半年的价格信息，格式为：时间戳+价格，数据参考如下

Prophet 要求数据必须包含两列：
- `ds`：日期时间列（datetime 格式）
- `y`：目标变量（需要预测的值）

1701360000000,23.60
1701499554000,23.60
1701532800000,23.60
1701619200000,23.60
1701705600000,23.60
1701802686000,27
1701878400000,27

……

（2）数据加载和预处理代码

加载数据文件并进行预处理

def load_data(file_path):
    """加载数据文件并进行预处理
    """
    # 读取数据，指定列名
    df = pd.read_csv(file_path, header=None, names=['timestamp', 'price'])
    
    # 将时间戳转换为日期时间
    df['ds'] = pd.to_datetime(df['timestamp'], unit='ms')
    
    # 确保价格为正数并移除异常值
    df['price'] = df['price'].clip(lower=0.01)
    
    # 计算移动平均和标准差
    df['price_ma'] = df['price'].rolling(window=7, min_periods=1).mean()
    df['price_std'] = df['price'].rolling(window=7, min_periods=1).std()
    
    # 使用Z-score方法移除异常值
    z_scores = stats.zscore(df['price'])
    df = df[abs(z_scores) < 3]  # 保留3个标准差以内的数据
    
    # 计算对数转换（对数变换可以使数据更稳定）
    df['y'] = np.log1p(df['price'])  # 使用log1p替代log
    
    # 按日期排序
    df = df.sort_values('ds')
    
    # 保存原始价格用于还原
    df['original_price'] = df['price']
    
    return df[['ds', 'y', 'original_price', 'price_ma', 'price_std']]

数据预处理的步骤：

  1. 将时间戳转换为 Prophet 要求的 ds 格式
  2. 对数据进行异常值处理（使用 Z-score 方法）
  3. 对价格进行对数变换，使数据更稳定
  4. 计算移动平均和标准差，用于后续分析

（3）模型配置与训练

创建并配置Prophet模型

# 创建并配置Prophet模型
model = Prophet(
    # 控制趋势变化的灵活度，值越小，趋势越稳定
    changepoint_prior_scale=0.001,
    
    # 控制季节性的强度，值越大，季节性影响越明显
    seasonality_prior_scale=10,
    
    # 季节性模式：multiplicative(乘法)表示季节性随趋势变化而变化
    seasonality_mode='multiplicative',
    
    # 是否考虑日度季节性，这里关闭因为价格不太可能每天都变
    daily_seasonality=False,
    
    # 是否考虑周度季节性，开启以捕捉每周的模式
    weekly_seasonality=True,
    
    # 是否考虑年度季节性，开启以捕捉每年的模式
    yearly_seasonality=True,
    
    # 预测区间的宽度，0.95表示95%置信区间
    interval_width=0.95,
    
    # 增长模式：linear表示线性增长
    growth='linear'
)

# 添加中国节假日因素，考虑节假日对价格的影响
model.add_country_holidays(country_name='CN')

# 添加月度季节性
model.add_seasonality(
    name='monthly',          # 季节性名称
    period=30.5,            # 周期天数（一个月平均天数）
    fourier_order=5         # 傅立叶级数阶数，控制季节性曲线的复杂度
)

# 训练模型
model.fit(df)

模型配置的关键参数：

  1. changepoint_prior_scale：控制趋势的灵活性，值越小趋势越平滑
  2. seasonality_prior_scale：控制季节性强度，值越大季节性越明显
  3. seasonality_mode：季节性模式，可以是加法或乘法
  4. growth：增长模式，可以是线性或逻辑增长

添加自定义季节性：

  • add_seasonality：添加自定义周期性，如月度季节性
  • add_country_holidays：添加特定国家的节假日效应

（4）生成预测

生成未来一年的日期序列用于预测

# 生成未来一年的日期序列用于预测
future_dates = model.make_future_dataframe(periods=365)

# 生成预测结果
forecast = model.predict(future_dates)

# 将预测值从对数空间转换回原始价格空间
forecast['yhat'] = inverse_transform_price(forecast['yhat'])
forecast['yhat_lower'] = inverse_transform_price(forecast['yhat_lower'])
forecast['yhat_upper'] = inverse_transform_price(forecast['yhat_upper'])

预测流程：

  1. 使用 make_future_dataframe 创建未来时间点
  2. 使用 predict 方法生成预测结果
  3. 将预测结果从对数空间转换回原始空间

（5）预测结果分析

分析月度价格统计数据

# 分析月度价格统计数据
monthly_stats = analyze_monthly_prices(forecast, df)
print("\n===== 月度价格预测 =====")
print(monthly_stats)

# 计算2025年的整体统计数据
forecast_2025 = forecast[forecast['ds'].dt.year == 2025]
mean_price = forecast_2025['yhat'].mean()
min_price = forecast_2025['yhat'].min()
max_price = forecast_2025['yhat'].max()
std_price = forecast_2025['yhat'].std()

# 输出年度统计结果
print("\n===== 年度价格统计 =====")
print(f"预测平均价格: {mean_price:.2f}")
print(f"预测最低价格: {min_price:.2f}")
print(f"预测最高价格: {max_price:.2f}")
print(f"价格标准差: {std_price:.2f}")
print(f"相对于当前价格变化: {((mean_price - current_price)/current_price*100):.1f}%")

结果分析包括：

  1. 月度统计：分析每月的平均价格、最高价格、最低价格和环比变化
  2. 年度统计：计算全年的平均价格、最高价格、最低价格和标准差
  3. 价格变化分析：计算预测价格相对于当前价格的变化百分比

（6）结果可视化

可视化预测结果及数据分析

def plot_price_prediction(model, forecast, history, product_name, output_file):
    """绘制价格预测图"""
    plt.figure(figsize=(15, 8))
    
    # 绘制历史数据
    plt.plot(history['ds'], history['original_price'], 
            label='历史价格', color='#2E86C1', linewidth=2)
    
    # 绘制历史移动平均线
    plt.plot(history['ds'], history['price_ma'],
            label='历史趋势', color='#27AE60', linewidth=1,
            linestyle='--', alpha=0.7)
    
    # 绘制预测数据
    future_mask = forecast['ds'] > history['ds'].iloc[-1]
    plt.plot(forecast.loc[future_mask, 'ds'], 
            forecast.loc[future_mask, 'yhat'],
            label='预测价格', color='#E74C3C', linewidth=2, 
            linestyle='--')
    
    # 绘制置信区间
    plt.fill_between(forecast.loc[future_mask, 'ds'],
                    forecast.loc[future_mask, 'yhat_lower'],
                    forecast.loc[future_mask, 'yhat_upper'],
                    color='#F1948A',
                    alpha=0.2,
                    label='95%置信区间')
    
    # 设置标题和标签
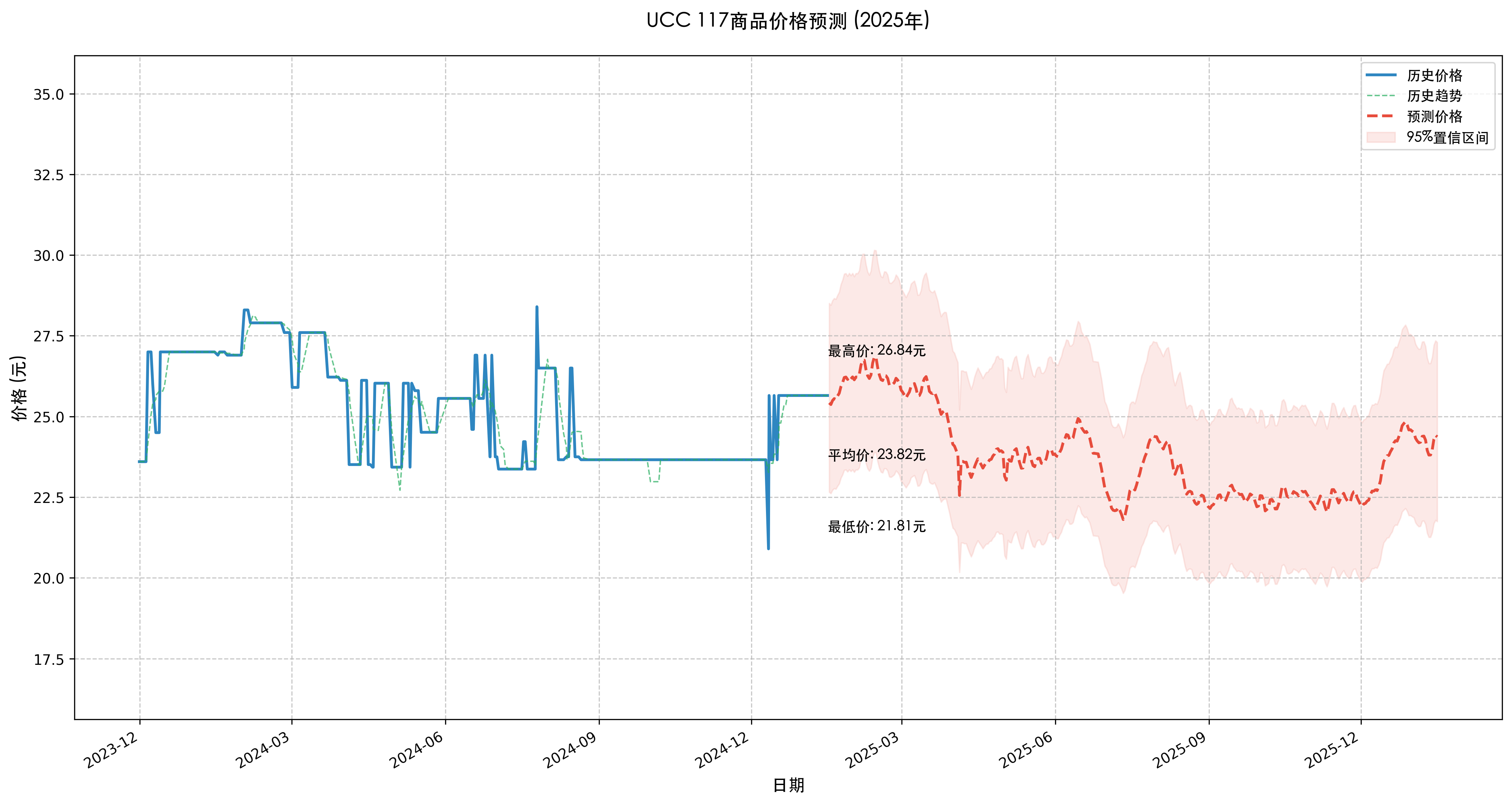
    plt.title(f'{product_name}商品价格预测 (2025年)')
    plt.xlabel('日期')
    plt.ylabel('价格 (元)')
    
    plt.legend()
    plt.savefig(output_file)

可视化内容包括：

  1. 历史价格数据和移动平均线
  2. 预测价格曲线
  3. 95% 置信区间
  4. 最高价格、最低价格和平均价格标注

（7）结果运行

执行程序，运行结果

2025-01  25.70  22.43  26.23  0.32      -     中
2025-02  26.29  23.00  26.84  0.28   2.3%     中
2025-03  25.54  21.55  26.24  0.50  -2.9%     中
2025-04  23.61  20.17  24.08  0.31  -7.6%     中
2025-05  23.68  20.58  24.05  0.24   0.3%     高
2025-06  24.14  20.37  24.94  0.51   1.9%     低
2025-07  22.94  19.52  24.40  0.87  -5.0%     低
2025-08  23.14  19.87  24.25  0.73   0.9%     低
2025-09  22.49  19.82  22.87  0.18  -2.8%     高
2025-10  22.49  19.76  22.83  0.21   0.0%     高
2025-11  22.42  19.73  22.73  0.18  -0.3%     高
2025-12  23.59  19.87  24.84  0.91   5.2%     低

===== 年度价格统计 =====
预测平均价格: 23.82
预测最低价格: 21.81
预测最高价格: 26.84
价格标准差: 1.36
相对于当前价格变化: -7.1%

得到预测图形如下

image.png

4. 获取资源

本文资料来源：

Discuss on Twitter • View on GitHub