Published on

蒙特卡罗方法：原理与Python实现

Authors
  • avatar
    Name
    Shoukai Huang
    Twitter
Monte Carlo method

蒙特卡罗方法（Photo by Stylite yu on Unsplash)

目录

1. 理论学习

1.1 核心概念

蒙特卡罗方法（英语：Monte Carlo method），也称统计模拟方法，是1940年代中期由于科学技术的发展和电子计算机的发明，而提出的一种以概率统计理论为指导的数值计算方法。这个方法的名字来源于摩纳哥著名的赌场"蒙特卡罗"，这个命名非常贴切，因为该方法利用随机性和概率来解决问题，就像赌场中的游戏一样充满了不确定性。

想象一下，如果你想知道掷骰子得到6点的概率，你可以理论计算（1/6），也可以实际掷骰子数千次，然后统计结果。蒙特卡罗方法就是采用后一种思路，通过大量重复试验来逼近问题的解。简单来说，蒙特卡罗方法就是使用随机数（或更常见的伪随机数）通过大量重复试验来解决复杂计算问题的方法。

通常蒙特卡罗方法可以粗略地分成两类：

第一类：直接模拟随机过程
这就像是模拟自然界中本来就随机的现象。例如，模拟放射性物质的衰变过程、股票市场的波动或者分子的热运动。在这些情况下，我们在计算机中创建一个"数字孪生"，让它按照真实世界的规则运行，然后观察结果。这就像是在电脑中创建了一个"平行宇宙"，让事件在其中自然发展。

第二类：转化为随机问题求解
这类问题本身可能并不随机，但我们可以巧妙地将其转化为随机问题。比如计算圆周率π，这本身是一个确定的数学常数，但我们可以通过随机投点的方式来估算它。这就像是用一种创造性的"迂回战术"来攻克那些用传统方法难以解决的问题。

假设我们要计算一个不规则图形的面积，那么图形的不规则程度和分析性计算（比如，积分）的复杂程度是成正比的。蒙特卡罗方法基于这样的想法：假设你有一袋豆子，把豆子均匀地朝这个图形上撒，然后数这个图形之中有多少颗豆子，这个豆子的数目就是图形的面积。当你的豆子越小，撒的越多的时候，结果就越精确。借助计算机程序可以生成大量均匀分布坐标点，然后统计出图形内的点数，透过它们占总点数的比例和坐标点生成范围的面积就可以求出图形面积。

1.2 工作过程

蒙特卡罗方法的工作流程可以比喻为科学实验的过程：

  1. 定义模型（实验设计）：就像科学家设计实验一样，我们需要明确问题的边界条件和规则。例如，如果要模拟城市交通，我们需要定义道路网络、车辆特性和驾驶行为规则等。

  2. 生成随机样本（准备实验材料）：这相当于准备实验所需的各种材料和条件。在蒙特卡罗模拟中，我们生成大量随机样本，代表不同的可能性或情景。

  3. 评估结果（进行实验）：将随机样本输入到模型中，让它们按照既定规则"运行"，然后记录每次模拟的结果。

  4. 分析结果（得出结论）：对大量模拟结果进行统计分析，计算平均值、方差等，从而得出关于系统行为的结论。

在解决实际问题的时候应用蒙特卡罗方法主要有两部分工作：

  1. 用蒙特卡罗方法模拟某一过程时，需要产生各种概率分布的随机变量。

  2. 用统计方法把模型的数字特征估计出来，从而得到实际问题的数值解。

1.3 方法特点

蒙特卡罗方法具有以下显著优点：

  1. 维度无关性：方法的误差与问题的维数无关，特别适合高维问题
  2. 统计问题直接求解：对于具有统计性质的问题可以直接进行解决
  3. 连续问题处理能力：对于连续性的问题不必进行离散化处理
  4. 复杂图形积分：能够比较逼真地描述具有随机性质的事物的特点及物理实验过程
  5. 几何限制小：受几何条件限制小
  6. 多方案计算能力：具有同时计算多个方案与多个未知量的能力
  7. 误差确定性：误差容易确定
  8. 实现简单：程序结构简单，易于实现

同时，蒙特卡罗方法也存在一些缺点：

  1. 问题转化需求：对于确定性问题需要转化成随机性问题
  2. 概率性误差：误差是概率误差，而非确定性误差
  3. 计算量大：通常需要较多的计算步数（N），收敛速度较慢
  4. 系统大小影响：在粒子输运问题中，计算结果与系统大小有关

使用建议：
在使用蒙特卡罗方法时，要"扬长避短"：

  • 只对问题中难以用解析（或数值）方法处理的部分使用蒙特卡罗方法计算
  • 对那些能用解析（或数值）方法处理的部分，应当尽量使用解析方法

2. 实践操作

2.1 估算π的值

估算π值是蒙特卡罗方法最经典的应用之一，它展示了如何将一个确定性问题转化为概率问题。这个方法背后的数学原理其实很简单：在一个边长为2的正方形内，我们可以画一个半径为1的圆。正方形的面积是4，而圆的面积是π。因此，随机点落在圆内的概率就是π/4。

通过计算机生成大量随机点，统计落在圆内的点的比例，再乘以4，我们就得到了π的近似值。这就像是用数字化的"飞镖游戏"来测量π值。随着投掷次数的增加，我们的估计会越来越准确。

让我们实现一个蒙特卡洛模拟来估算π的值。我们将使用经典方法，模拟单位正方形内的随机点，并检查有多少个点落在四分之一圆内。

我们将遵循以下步骤：

  1. 生成随机点：我们在单位正方形内生成随机 x 和 y 坐标。
  2. 计算距离：计算每个点与原点的距离。
  3. 计算圆内的点数：确定四分之一圆内有多少个点。
  4. 估算π：利用圆内的点数与总点数的比例来估算π。
import numpy as np
import matplotlib.pyplot as plt

def monte_carlo_pi(num_samples):
    # 生成随机点
    x = np.random.uniform(-1, 1, num_samples)
    y = np.random.uniform(-1, 1, num_samples)
    
    # 计算每个点到原点的距离
    distance = np.sqrt(x**2 + y**2)
    
    # 统计落在单位圆内的点数
    inside_circle = np.sum(distance <= 1)
    
    # 估算π值
    pi_estimate = (inside_circle / num_samples) * 4
    
    return pi_estimate

# 样本数量
num_samples = 10000

# 运行蒙特卡罗模拟
pi_estimate = monte_carlo_pi(num_samples)

print(f"使用{num_samples}个样本估算的π值: {pi_estimate}")

# 可视化：绘制随机点分布
x = np.random.uniform(-1, 1, num_samples)
y = np.random.uniform(-1, 1, num_samples)
plt.figure(figsize=(6, 6))
plt.scatter(x, y, c=np.sqrt(x**2 + y**2) <= 1, cmap='bwr', s=1)
plt.gca().set_aspect('equal', adjustable='box')
plt.title('Monte Carlo Simulation for π')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

jupyter notebook 运行结果

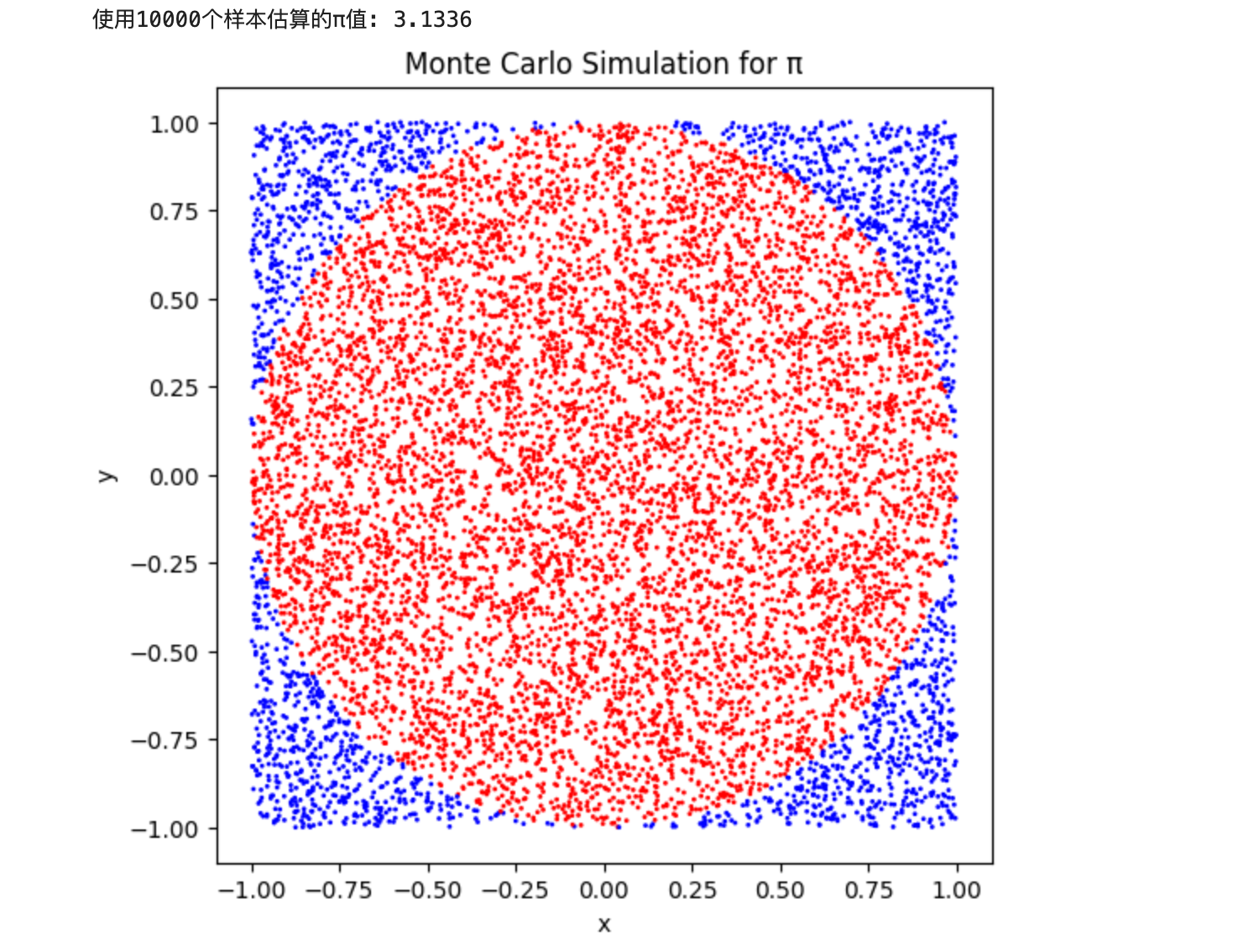
Monte Carlo Simulation for π

2.2 估算积分

积分计算在数学和物理中非常重要，但解析解并不总是容易获得。蒙特卡罗积分方法提供了一种通用的数值解法。

对于函数f(x)在区间[a,b]上的积分，我们可以将其视为计算区间上函数曲线下方的面积。蒙特卡罗方法的思路是：在区间[a,b]上随机生成x值，计算对应的f(x)，然后取平均值乘以区间长度(b-a)。

这就像是在函数图像上随机采样一些点，然后用这些点的高度的平均值来估计整体的平均高度。采样点越多，估计就越准确。这种方法特别适合处理高维积分问题，因为它的计算复杂度不会随着维度的增加而爆炸性增长。

我们要评估的积分是：

∫0πsin⁡x dx\int_{0}^{\pi} \sin x \, dx

我们将遵循以下步骤：

  1. 定义积分区间：确定我们要计算的积分的上下限。
  2. 生成随机样本：在积分区间内生成均匀分布的随机点。
  3. 评估函数值：计算每个随机点对应的函数值。
  4. 估算积分：根据随机采样的平均函数值乘以区间长度来估算积分值。
# 导入必要的模块
import numpy as np
import matplotlib.pyplot as plt

# 积分区间的上下限
a = 0
b = np.pi # 获取π的值
N = 1000

# 定义函数计算特定x值的正弦值
def f(x):
    return np.sin(x)

# 创建列表存储所有计算结果用于绘图
plt_vals = []

# 我们进行多次迭代以生成多个结果
# 并展示哪个结果出现频率最高
for i in range(N):
  
    # 创建长度为N的零数组
    ar = np.zeros(N)

    # 遍历数组中的每个元素并填充
    # 用区间[a,b]内的随机值
    for i in range (len(ar)):
        ar[i] = np.random.uniform(a,b)

    # 变量用于存储不同x值对应函数值的总和
    integral = 0.0

    # 遍历并累加不同x值对应的函数值
    for i in ar:
        integral += f(i)

    # 使用推导出的公式计算结果
    ans = (b-a)/float(N)*integral

    # 将计算结果添加到列表中用于绘制图表
    plt_vals.append(ans)

# 设置绘图细节
# 设置图表标题
plt.title("Distributions of areas calculated")

# 绘制直方图，参数说明：数据数组、分箱数量、分隔线颜色
plt.hist (plt_vals, bins=30, ec="black") 

# 设置x轴标签
plt.xlabel("Areas")
plt.show() # 显示图表

jupyter notebook 运行结果

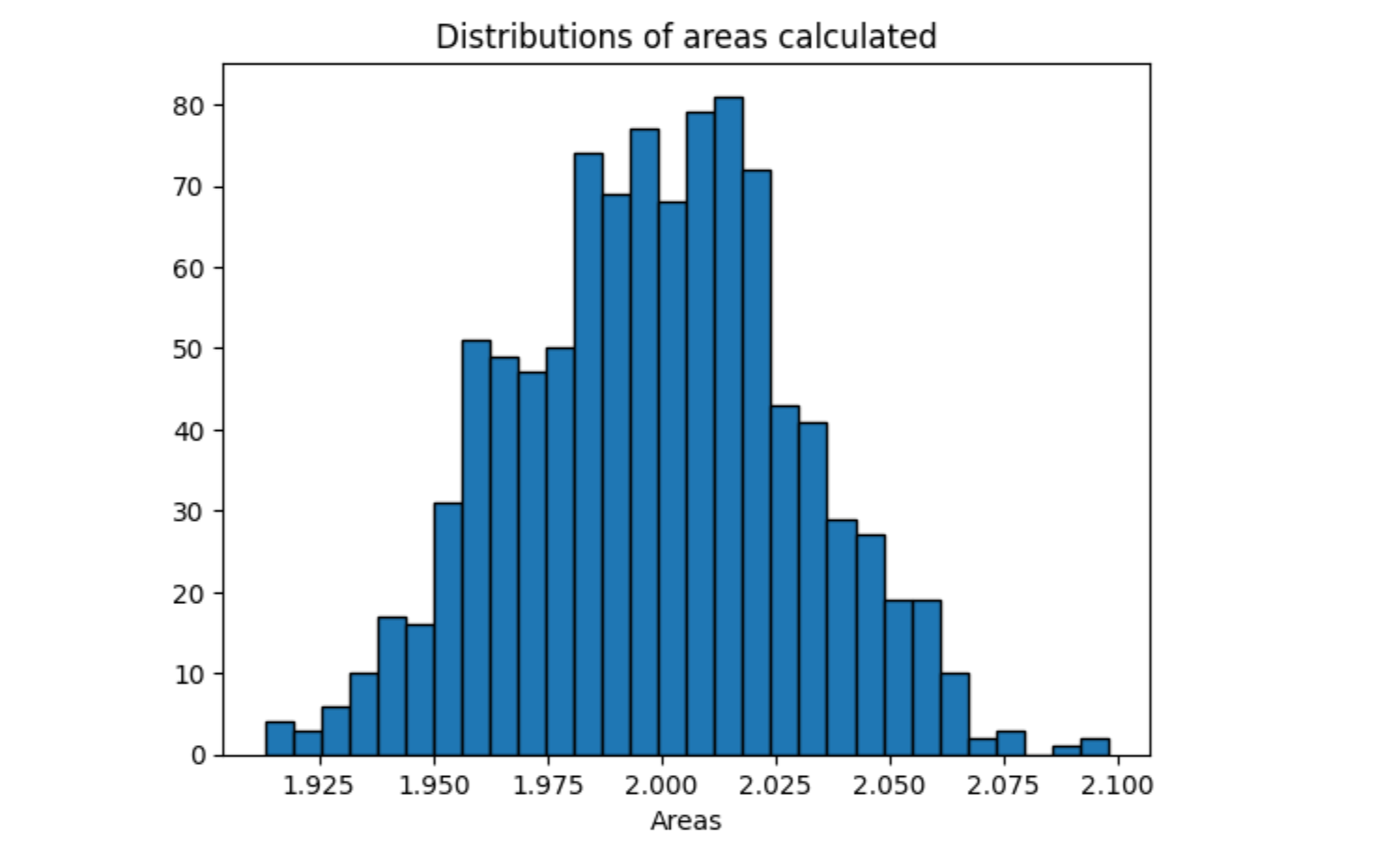
Distributions of areas calculated

从上图可以看出，根据直方图显示，最可能的计算结果约为1.975或2.025，这与该积分的实际解析解2.0非常接近。这证明了蒙特卡罗方法在数值积分中的有效性。

2.3 蒙特卡罗方法在强化学习中的应用

蒙特卡罗方法在强化学习中有着广泛的应用，特别是在估计状态价值函数和动作价值函数方面。与动态规划和时序差分学习不同，蒙特卡罗方法不需要环境模型，而是通过实际经验来学习。

在强化学习中，蒙特卡罗方法的基本思想是：

  1. 通过与环境交互，收集完整的状态-动作-奖励序列（称为轨迹或情节）
  2. 对每个状态或状态-动作对，计算其回报（未来奖励的折扣和）
  3. 通过多次采样，估计每个状态或状态-动作对的期望回报

蒙特卡罗方法的优点在于它可以从实际经验中学习，不需要环境模型，并且能够处理非马尔可夫环境。但缺点是需要等到情节结束才能更新价值函数，这可能导致学习效率较低。

在实际应用中，蒙特卡罗方法常用于：

  • 策略评估：估计给定策略下的状态价值函数
  • 策略改进：基于价值函数估计来改进策略
  • 探索起始：在未知环境中进行初始探索

参考