Q-Learning 精解：从数学原理到代码实现的深度探索

Q-Learning（Photo by Norbert Levajsics on Unsplash)

1. 基础研究

1.1 强化学习

强化学习（Reinforcement Learning, RL）作为机器学习的重要分支，其核心范式是智能体（Agent）通过与动态环境的持续交互，从反馈奖励中自主学习最优决策策略。与监督学习依赖标注数据不同，强化学习更接近生物进化中的"试错学习"机制，通过探索与利用的平衡来适应未知环境，特别适用于机器人控制、游戏AI、资源调度等序列决策问题。

在强化学习框架中，智能体通过探索（尝试新动作）与利用（选择已知高回报动作）的平衡策略与环境交互，根据延迟奖励信号调整行为模式，最终学习到能最大化长期累积奖励的最优策略。这一学习范式与人类和动物的自然学习过程高度相似，使其成为人工智能领域中最接近自然智能的学习方法之一。

强化学习的核心要素

智能体（Agent）：做出决策并执行动作的实体
环境（Environment）：智能体所处的外部系统
状态（State）：环境在特定时刻的表征
动作（Action）：智能体可以执行的操作
奖励（Reward）：环境对智能体行为的即时反馈
策略（Policy）：智能体的决策规则，决定在给定状态下应采取什么动作

强化学习基本流程

强化学习的典型交互循环可概括为以下步骤：

智能体观察当前环境状态
基于特定策略选择并执行动作
环境根据智能体的动作转换到新状态
智能体接收奖励信号
智能体根据获得的经验更新其策略
重复上述过程，直至找到最优策略

这一过程通常会重复数千甚至数百万次，直到智能体学会在各种状态下做出最优决策。

1.2 冰冻湖面环境

为了具体理解强化学习的应用，我们将聚焦于OpenAI Gym提供的经典环境——冰冻湖面（FrozenLake）。这是一个简单而富有挑战性的环境，非常适合初学者理解强化学习的基本概念。

center

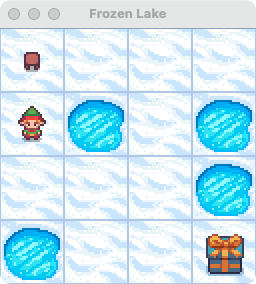
冰冻湖面环境示意图（Photo by Gymnasium Gymnasium)

环境描述

冰冻湖面是一个4×4的网格世界，包含以下元素：

起点（S）：智能体的初始位置，位于网格的左上角
终点（G）：智能体的目标位置，位于网格的右下角
冰洞（H）：危险区域，智能体落入即失败
冰面（F）：安全区域，智能体可以在其上移动

智能体的任务是从起点出发，在不掉入冰洞的前提下到达终点。这个看似简单的任务因为环境的随机性（冰面可能很滑）而变得颇具挑战性。

状态与动作空间

状态空间：共16个状态（0-15），对应网格中的每个位置
动作空间：4个动作（0-3），分别对应上、右、下、左四个移动方向
奖励设置：
- 到达终点：+1
- 掉入冰洞或其他移动：0

使用 OpenAI Gym 建环境

OpenAI Gym提供了便捷的接口来创建和交互冰冻湖面环境，如下展示如何通过最简化代码运行环境

"""
FrozenLake环境演示
这个脚本演示了如何使用OpenAI Gym的FrozenLake环境，并提供了可视化界面
"""
import gymnasium as gym
import time

def run_random_agent():
    """演示随机智能体在FrozenLake环境中的表现"""
    # 创建环境，使用human渲染模式以显示界面
    env = gym.make("FrozenLake-v1", map_name="4x4", is_slippery=False, render_mode="human")
    
    # 重置环境
    state, _ = env.reset()
    
    # 运行随机智能体
    done = False
    total_reward = 0
    
    print("演示开始: 随机智能体在冰冻湖面环境中")
    print("目标: 从起点(S)移动到目标(G)，同时避开洞(H)")
    print("控制: 程序自动执行随机动作")
    print("按窗口的关闭按钮可以退出演示")
    
    # 渲染初始状态
    env.render()
    time.sleep(0.5)  # 给用户一些时间看初始状态
    
    while not done:
        # 随机选择动作
        action = env.action_space.sample()
        
        # 执行动作
        next_state, reward, terminated, truncated, _ = env.step(action)
        done = terminated or truncated
        total_reward += reward
        
        # 渲染环境
        env.render()
        
        # 暂停一下，让用户能看清动作
        time.sleep(0.3)
        
        # 更新状态
        state = next_state
    
    # 如果环境结束，显示最终状态一段时间
    if done:
        time.sleep(2)  # 显示最终状态2秒
    
    # 关闭环境
    env.close()
    print(f"演示结束! 总奖励: {total_reward}")

if __name__ == "__main__":
    print("冰冻湖面环境演示 - 随机智能体")
    print("使用Gym自带的渲染功能")
    run_random_agent()

通过Gym环境，我们可以轻松获取环境的观察空间、动作空间以及与环境交互所需的各种方法。

> python frozen_lake_demo.py

冰冻湖面环境演示 - 随机智能体
演示开始: 随机智能体在冰冻湖面环境中
目标: 从起点(S)移动到目标(G)，同时避开洞(H)
控制: 程序自动执行随机动作
按窗口的关闭按钮可以退出演示
演示结束! 总奖励: 0.0

运行结果如下：

注：本文使用的是 conda 环境，uv 由于 pytorch 的没有适用于该平台的源发行版，未安装成功。

You're on macOS (macosx_12_0_x86_64), but torch (v2.7.1) only has wheels for the following platforms: manylinux_2_28_aarch64, manylinux_2_28_x86_64, macosx_11_0_arm64, win_amd64

1.3 Q-Table：知识表征的核心数据结构

在Q-Learning算法中，Q-Table（Q表）是存储和更新智能体知识的关键数据结构。它本质上是一个查找表，记录了在每个状态下执行各种动作的预期价值。

Q表的结构与初始化

Q表是一个二维矩阵，其中：

行数等于状态空间的大小
列数等于动作空间的大小
每个单元格Q(s,a)表示在状态s下执行动作a的预期长期回报

对于冰冻湖面环境，我们需要一个16×4的Q表：

import numpy as np

# 初始化Q表，所有值设为0
state_space = 16  # 16个状态
action_space = 4  # 4个动作
q_table = np.zeros((state_space, action_space))

注意，这块 q_table 的大小是 16*4，总空间大小是：状态空间数量 * 动作空间数量。

初始时，所有Q值被设置为0，表示智能体对环境一无所知。随着学习的进行，Q表将逐渐被更新，反映智能体对环境的理解。

1.4 贝尔曼方程：强化学习的数学基石

贝尔曼方程是动态规划和强化学习的理论基石，由美国数学家理查德·贝尔曼（Richard Bellman）提出。它提供了一种递归方式来描述最优决策问题，是Q-Learning算法的核心数学基础。

贝尔曼最优方程

对于动作值函数Q(s,a)，贝尔曼最优方程可表示为：

V(s) = \max_{a} \left( R(s, a) + \gamma \sum_{s'} P(s' \mid s, a) V(s') \right)

符号解释

符号	含义
`V(s)`	状态 `s` 的最优值函数：从状态 `s` 出发，遵循最优策略能获得的期望累积回报
`maxₐ`	对所有可能动作取最大值：选择使长期回报最大化的动作
`R(s, a)`	即时奖励：在状态 `s` 执行动作 `a` 后获得的直接奖励
`γ`	折扣因子 (`0 ≤ γ < 1`)：平衡当前奖励与未来奖励的重要性
`∑ₛ'`	对所有可能的下一个状态 `s'` 求和
`P(s'∣s, a)`	转移概率：在状态 `s` 执行动作 `a` 后转移到状态 `s'` 的概率
`V(s')`	后继状态 `s'` 的最优值函数：表示未来的期望回报

关键说明

最优决策核心
maxₐ 确保智能体始终选择最大化长期累积回报的动作（而非仅即时奖励）
时间分解原理
- 即时奖励：当前动作带来的直接收益 (R(s,a))
- 未来折扣回报：所有可能后续状态的期望值 (γ∑P(s'∣s,a)V(s'))
动态系统特性
- 通过转移概率 P(s'∣s,a) 建模环境的不确定性
- 递归关联当前状态值与后续状态值
实际求解方法
- 值迭代算法：通过循环更新 V(s) 直至收敛
- 当 γ < 1 时保证唯一解和收敛性
- 解出 V(s) 后即可导出最优策略 π*(s) = argmaxₐ[...]
策略优化本质
- 该方程同时隐含定义了最优策略： $\pi^*(s) = \underset{a}{\mathrm{argmax}} \left( R(s,a) + \gamma \sum_{s'} P(s'|s,a) V(s') \right)$ 即选择使状态动作值最大化的动作

在Q-Learning中，我们不需要知道转移概率 $P(s'|s,a)$ ，而是通过实际交互来学习Q值，这使其成为一种"无模型"（model-free）的强化学习方法。

贝尔曼方程的核心思想是：当前状态-动作对的价值等于即时奖励加上折扣后的下一状态最大价值。这一递归关系为Q-Learning算法提供了理论基础，也是Q表更新的数学依据。

在下一部分，我们将深入探讨Q-Learning算法，以及如何将这些理论概念应用到冰冻湖面环境的实际问题中。

2. Q-Learning算法

2.1 Q-Learning的本质

Q-Learning作为一种经典的强化学习算法，其核心在于通过交互式学习构建最优决策策略，而无需事先了解环境模型（即"无模型"方法）。该算法的独特之处在于能够处理具有随机转换和奖励的复杂环境，通过试错学习找到最优解。

算法核心思想

Q-Learning的核心思想是维护一个状态-动作值函数（Q函数），它估计在给定状态下执行特定动作的长期价值。随着智能体与环境的不断交互，这些估计值会逐渐收敛到真实值，从而指导智能体做出最优决策。

以网格迷宫为例：智能体的目标是找到通往出口（奖励为10分）的最短路径。在每个交叉路口，Q-Learning会为不同方向的移动赋予不同的价值。如果右转能更快到达出口，随着学习的进行，右转动作的Q值将高于左转，从而引导智能体选择最优路径。

理论保证

Q-Learning的理论基础十分扎实：对于任何有限马尔可夫决策过程(MDP)，在给定足够的探索时间和部分随机策略的条件下，Q-Learning能够确定最优行动策略，即从当前状态开始，最大化所有后续步骤的总期望奖励。

名称"Q"来源于算法计算的函数：Quality of Action（动作的质量）—在给定状态下采取特定动作的预期长期回报。

2.2 Q-Learning的工作机制

Q表：知识的存储结构

Q表是Q-Learning算法的核心数据结构，它是一个二维矩阵，行表示所有可能的状态，列表示每个状态下可执行的动作，每个单元格存储对应状态-动作对的Q值。

对于冰冻湖面环境，Q表的维度为16×4，对应16个可能的位置状态和4个可能的移动方向。初始时，所有Q值通常被设置为0，表示智能体对环境一无所知。随着学习的进行，Q表会不断更新，逐渐反映智能体对环境的理解。

Q函数与贝尔曼方程

Q函数基于贝尔曼最优方程，该方程提供了一种递归方式来计算状态-动作对的价值：

$Q(s,a) = R(s,a) + \gamma \max_{a'} Q(s',a')$

符号	含义
`Q(s,a)`	状态-动作值函数：在状态 `s` 执行动作 `a` 的预期长期回报
`R(s,a)`	即时奖励：执行动作 `a` 后立即获得的奖励
`γ`	折扣因子 (`0 ≤ γ < 1`)：未来奖励的衰减系数
`s'`	后继状态：执行动作 `a` 后转移到的下一状态
`maxₐ' Q(s',a')`	最优未来价值：在 `s'` 状态下所有可能动作的最大 Q 值

Q值更新规则

在实际应用中，Q值通过以下公式迭代更新：

Q-learning 更新公式
$Q(s,a) \leftarrow Q(s,a) + \alpha \left[ r + \gamma \max_{a'} Q(s',a') - Q(s,a) \right]$

符号解释

符号	含义
`Q(s,a)`	更新前的状态-动作值（当前估计值）
`α` (alpha)	学习率 (`0 < α ≤ 1`)：控制新信息对Q值的影响程度。
`r`	实际获得的即时奖励：执行动作后观测到的真实奖励
`γ` (gamma)	折扣因子 (`0 ≤ γ < 1`)：平衡即时与未来奖励的权重。
`maxₐ' Q(s',a')`	下一状态最优Q值：在新状态 `s'` 所有可能动作中的最大Q值
`s'`	实际转移到的状态：执行动作后观测到的下一个状态
`[ ]` 内整体	时间差分误差 (TD error)：新估计与旧估计的差值

其中：

α=0.1~0.5为常用范围，值越大学习速度越快但可能导致震荡，值越小收敛更稳定但学习速度减慢；
γ=0.9~0.99为常用范围，值接近1时智能体更注重长期回报，值较小时更关注短期收益；

更新规则详解

核心思想：增量学习
- 通过实际经验 (s,a,r,s') 逐步修正Q值估计
- 类似"预测误差修正"：新Q值 = 旧Q值 + α × (新估计 - 旧估计)
时间差分误差 (TD error)
δ = r + γ maxₐ' Q(s',a') - Q(s,a) 包含：
- 实际即时奖励 r（真实反馈）
- 最优未来价值 γ maxₐ' Q(s',a')（当前预测）
- 减去原估计 Q(s,a)（形成误差项）
学习率 α 的作用

\begin{cases} α = 0 & \text{→ Q值完全不更新} \\ α = 1 & \text{→ 完全替换为 } Q_{\text{new}} = r + \gamma \max_{a'} Q(s',a') \\ 0<α<1 & \text{→ 新旧估计加权平均（常用0.1）} \end{cases}

更新流程

每次从状态 s 执行动作 a 后：

观测 → 获得奖励 r 和新状态 s'
计算目标值 → target = r + γ maxₐ' Q(s',a')
计算误差 → δ = target - Q(s,a)
更新Q表 → Q(s,a) += α × δ

收敛保证

当满足以下条件时，Q值收敛到最优解：

充分探索：访问所有状态-动作对无限次
学习率调整：满足 Robbins-Monro 条件： $\begin{cases} \sum_{t=1}^{\infty} \alpha_t = \infty \\ \sum_{t=1}^{\infty} \alpha_t^2 < \infty \end{cases}$ （例如使用衰减策略 αₜ = 1/t 或 αₜ = 1/(1 + k·t)）

学习率衰减示例

# Python 实现学习率衰减
# 学习率控制新经验对Q值的影响程度
# 高学习率(接近1)使新经验权重更大，低学习率使学习更稳定
alpha_init = 0.5  # 初始学习率

for episode in range(1, 10001):
    # 1/k衰减方案：随训练进行逐渐降低学习率
    # 确保满足Robbins-Monro收敛条件
    alpha = alpha_init / episode
    
    # 另一种常用衰减方案：线性衰减
    # alpha = 1 / (1 + 0.001 * episode)
    
    # 在Q更新中使用当前alpha
    # 新Q值 = 旧Q值 + 学习率 × 时间差分误差
    Q[s][a] += alpha * (target - Q[s][a])

这个更新规则体现了Q-Learning的核心思想：通过实际交互经验不断调整对状态-动作价值的估计，逐步接近最优策略。

2.3 Q-Learning的关键策略平衡

探索与利用的平衡

Q-Learning面临的一个核心挑战是探索（exploration）与利用（exploitation）之间的平衡：

探索：尝试新的、可能次优的动作，以发现潜在的更好策略
利用：基于当前知识选择最优动作，最大化短期回报

常用的平衡策略是ε-贪婪（epsilon-greedy）策略，通过动态调整探索概率实现智能平衡：

探索阶段（初期）：ε=1.0 → 完全随机选择动作，帮助智能体了解环境全貌
过渡阶段（中期）：ε线性/指数衰减 → 逐渐减少探索比例
利用阶段（后期）：ε=0.01~0.1 → 主要依赖学习到的Q值决策，仅保留少量探索

ε衰减示例：

指数衰减：ε = ε_min + (ε_max - ε_min) × exp(-decay_rate × episode)
线性衰减：ε = max(ε_min, ε_max - (ε_max-ε_min)×(episode/total_episodes))

这种策略确保智能体初期充分探索环境，后期专注于利用最优策略，有效解决了探索-利用困境。

def epsilon_greedy_policy(Qtable, state, epsilon):
    if random.uniform(0, 1) > epsilon:
        # 利用：选择Q值最高的动作
        action = np.argmax(Qtable[state])
    else:
        # 探索：随机选择动作
        action = random.randint(0, action_space-1)
    return action

Q-Learning算法步骤

完整的Q-Learning算法可概括为以下步骤：

初始化：为所有状态-动作对(s,a)初始化Q表，通常设置Q(s,a) = 0
对于每个回合（episode）：
- 初始化起始状态s
- 对于每一步，直到达到终止状态：
  - 使用ε-贪婪策略根据当前Q值选择动作a
  - 执行动作a，观察奖励r和新状态s'
  - 更新Q值：Q(s,a) ← Q(s,a) + α[r + γ·max_a'Q(s',a') - Q(s,a)]
  - s ← s'（状态转移）

随着回合数的增加，Q表会逐渐收敛到最优值，从而能够指导智能体在任何状态下做出最优决策。

2.4 Q-Learning的核心术语

理解以下关键概念对于掌握Q-Learning算法至关重要：

Q值（动作值）：表示在特定状态下采取特定动作的长期价值，估计从该状态出发，采取该动作并遵循最优策略可获得的未来预期奖励总和。
状态（State）：环境在特定时刻的表征，是智能体做出决策的依据。在冰冻湖面环境中，状态对应网格中的16个位置。
动作（Action）：智能体可以执行的操作，影响环境状态的转变。在冰冻湖面环境中，动作包括上、右、下、左四个移动方向。
奖励（Reward）：环境对智能体行为的即时反馈，引导智能体学习期望的行为。在冰冻湖面环境中，到达终点获得+1奖励，其他情况为0。
策略（Policy, π）：智能体的决策规则，决定在每个状态下应采取什么动作。在Q-Learning中，最优策略通常是在每个状态下选择Q值最高的动作。
学习率（α）：控制新知识更新速度的参数。学习率越高，智能体学习越快，但可能导致不稳定；学习率越低，学习越稳定但速度较慢。
折扣因子（γ）：平衡即时奖励与未来奖励重要性的参数。γ越接近1，智能体越重视长期回报；γ越接近0，智能体越注重即时奖励。
回合（Episode）：从初始状态到终止状态的完整交互序列。在冰冻湖面环境中，一个回合从起点开始，到达终点或掉入冰洞结束。
收敛（Convergence）：随着学习的进行，Q值逐渐稳定到最优值的过程。当Q表收敛后，智能体能够在任何状态下做出最优决策。

2.5 Q-Learning的边界

尽管Q-Learning在解决强化学习问题方面表现出色，但它也存在一些固有的局限性：

维度灾难：当状态或动作空间非常大时，Q表变得不可行。例如，在围棋这样的游戏中，状态空间约为10^170，无法用传统Q表表示。
泛化能力差：传统Q-Learning对于未见过的状态无法做出良好预测，每个状态-动作对都需要单独学习，缺乏状态间的知识迁移。
收敛速度慢：在复杂环境中，Q-Learning可能需要大量样本才能收敛到最优策略，这在实际应用中可能不切实际。
离散空间限制：传统Q-Learning主要适用于离散状态和动作空间，对于连续空间需要进行离散化处理，可能导致信息损失。

3. Q-Learning 实战

本节将 Q-Learning 理论转化为可执行代码，通过FrozenLake环境的实践案例，展示强化学习算法的完整实现流程与关键技术细节。

3.1 技术准备

首先，我们需要导入必要的库：

import numpy as np
import random
import matplotlib.pyplot as plt
import gymnasium as gym

numpy (np): 用于高效的数值计算和数组操作
random: 生成随机数，用于探索策略
matplotlib.pyplot: 数据可视化工具
gymnasium: OpenAI Gym 的继承者，提供强化学习环境

3.2 Epsilon-Greedy策略

Epsilon-Greedy 策略是强化学习中常用的平衡探索与利用的方法。该策略以 ε 的概率随机选择动作（探索），以 1-ε 的概率选择当前状态下 Q 值最大的动作（利用）。

def epsilon_greedy_policy(Qtable, state, epsilon):
    """
    ε-贪婪策略实现探索与利用的平衡
    参数:
        Qtable: 状态-动作价值表
        state: 当前环境状态
        epsilon: 探索概率阈值
    返回:
        action: 选择的动作
    """
    # 生成0-1随机数，决定当前是探索还是利用
    exploration_exploitation_tradeoff = random.uniform(0, 1)
    
    # 利用(exploitation): 选择当前状态下Q值最高的动作
    if exploration_exploitation_tradeoff > epsilon:
        action = np.argmax(Qtable[state])
    # 探索(exploration): 随机选择一个动作
    else:
        action = random.randint(0, Qtable.shape[1]-1)  # 动态适应动作空间大小
    return action

这个函数接收三个参数：

Qtable: 存储所有状态-动作对应的 Q 值
state: 当前状态
epsilon: 探索概率

函数首先生成一个 0 到 1 之间的随机数，如果该数大于 epsilon，则选择 Q 值最大的动作（利用）；否则，随机选择一个动作（探索）。

3.3 Q-Learning 算法实现

Q-Learning 是一种无模型（model-free）的强化学习算法，通过不断更新 Q 表来学习最优策略。

初始化

# 初始化 Q-Table
state_space = 16  # 16 个状态
action_space = 4  # 4 个动作
Qtable = np.zeros((state_space, action_space))

# 训练参数及调优建议
n_training_episodes = 10000  # 训练回合数：复杂环境需增加至10^5量级
learning_rate = 0.7          # 学习率：建议0.1~0.5，环境噪声大时取较小值
gamma = 0.95                 # 折扣因子：短期奖励重要取0.7~0.9，长期规划取0.9~0.99
max_steps = 99               # 每回合最大步数：应大于环境最短解决路径长度
max_epsilon = 1.0            # 初始探索概率：通常设为1.0
min_epsilon = 0.05           # 最小探索概率：保留0.01~0.1以应对环境变化
decay_rate = 0.0005          # 探索概率衰减率：1e-3~1e-4，控制衰减速度

# 参数调优原则
# 1. 学习不稳定时：减小学习率，增加训练回合数
# 2. 收敛速度慢时：适当增大学习率，检查gamma是否过小
# 3. 策略震荡时：减小学习率，增加epsilon最小值
# 4. 无法找到最优解：检查max_steps是否足够，增加探索强度

# 初始化环境
env = gym.make('FrozenLake-v1', is_slippery=False)

这里我们：

创建一个 16×4 的 Q 表，对应 FrozenLake 环境中的 16 个状态和 4 个可能的动作
设置训练参数，包括学习率、折扣因子、探索概率等
初始化 FrozenLake 环境，并设置为不滑动模式

训练循环

# 训练主循环
for episode in range(n_training_episodes):
    # 重置环境，获取初始状态
    state, _ = env.reset()
    step = 0
    done = False
    
    # 指数衰减策略计算当前epsilon
    # 初期高探索(高ε)，后期高利用(低ε)
    epsilon = min_epsilon + (max_epsilon - min_epsilon) * np.exp(-decay_rate * episode)

    while not done and step < max_steps:
        # 1. 根据ε-贪婪策略选择动作
        action = epsilon_greedy_policy(Qtable, state, epsilon)
        
        # 2. 执行动作，与环境交互
        new_state, reward, terminated, truncated, info = env.step(action)
        done = terminated or truncated  # 终止条件判断
        
        # 3. Q-Learning核心更新公式
        # Q(s,a) ← Q(s,a) + α[r + γ·max_a'Q(s',a') - Q(s,a)]
        # 其中[r + γ·max_a'Q(s',a')]是目标Q值，[r + γ·max_a'Q(s',a') - Q(s,a)]是时间差分误差
        Qtable[state, action] += learning_rate * (reward + gamma * np.max(Qtable[new_state]) - Qtable[state, action])
        
        # 4. 状态转移
        state = new_state
        step += 1
    
    # 每1000回合打印训练进度
    if (episode + 1) % 1000 == 0:
        print(f"训练进度: {episode+1}/{n_training_episodes}回合, 当前ε值: {epsilon:.4f}")

训练过程包括：

对每个训练回合，重置环境获取初始状态
计算当前回合的 epsilon 值（随着训练进行，探索概率逐渐减小）
在每个步骤中：
- 使用 epsilon-greedy 策略选择动作
- 执行动作，获取新状态和奖励
- 使用 Q-Learning 更新公式更新 Q 表
- 转移到新状态

Q-Learning 的核心更新公式为：

Q(s,a) = Q(s,a) + α * (r + γ * max(Q(s')) - Q(s,a))

其中：

Q(s,a) 是状态 s 下采取动作 a 的 Q 值
α 是学习率
r 是即时奖励
γ 是折扣因子
max(Q(s')) 是下一状态 s' 的最大 Q 值

3.4 模型评估

训练完成后，我们需要评估模型的性能：

def evaluate_agent(Qtable, n_eval_episodes=100):
    """
    评估训练后智能体的性能
    参数:
        Qtable: 训练好的Q表
        n_eval_episodes: 评估回合数
    返回:
        mean_reward: 平均奖励值
    """
    total_rewards = []
    for episode in range(n_eval_episodes):
        state, _ = env.reset()  # 重置环境
        total_reward = 0
        done = False
        while not done:
            # 纯利用策略：始终选择Q值最高的动作
            action = np.argmax(Qtable[state])
            new_state, reward, terminated, truncated, info = env.step(action)
            done = terminated or truncated
            total_reward += reward
            state = new_state
        total_rewards.append(total_reward)
    # 计算平均奖励作为评估指标
    mean_reward = np.mean(total_rewards)
    return mean_reward

n_eval_episodes = 100
mean_reward = evaluate_agent(Qtable, n_eval_episodes)
print(f"{n_eval_episodes}个回合的平均奖励: {mean_reward:.2f}")

评估过程中，我们：

运行多个评估回合
在每个回合中，始终选择 Q 值最大的动作（纯利用策略）
记录每个回合获得的总奖励
计算平均奖励作为模型性能的指标

3.5 结果可视化

最后，我们可以可视化智能体在环境中的行为：

def visualize_path(Qtable):
    """
    可视化智能体在环境中的决策路径
    参数:
        Qtable: 训练好的Q表
    返回:
        path: 智能体走过的状态序列
    """
    state, _ = env.reset()
    path = [state]  # 记录路径的状态序列
    done = False
    while not done:
        # 基于Q表选择最优动作
        action = np.argmax(Qtable[state])
        new_state, reward, terminated, truncated, info = env.step(action)
        done = terminated or truncated
        path.append(new_state)
        state = new_state
    return path

path = visualize_path(Qtable)
print("智能体走过的路径:", path)

这个函数记录了智能体从起点到终点的路径，帮助我们直观地理解学习到的策略。

3.6 完整代码：Q-Learning的一体化实现

以下是完整的 Q-Learning 实现代码：

import numpy as np
import random
import matplotlib.pyplot as plt
import gymnasium as gym

# 初始化 Q-Table
state_space = 16  # 16 个状态
action_space = 4  # 4 个动作
Qtable = np.zeros((state_space, action_space))

def epsilon_greedy_policy(Qtable, state, epsilon):
    random_int = random.uniform(0, 1)
    if random_int > epsilon:
        action = np.argmax(Qtable[state])  # 开发（利用已知信息）
    else:
        action = random.randint(0, 3)  # 探索（随机选择动作）
    return action

def evaluate_agent(Qtable, n_eval_episodes=100):
    total_rewards = []
    for episode in range(n_eval_episodes):
        state, _ = env.reset()
        total_reward = 0
        done = False
        while not done:
            action = np.argmax(Qtable[state])
            new_state, reward, terminated, truncated, info = env.step(action)
            done = terminated or truncated
            total_reward += reward
            state = new_state
        total_rewards.append(total_reward)
    mean_reward = np.mean(total_rewards)
    return mean_reward

def visualize_path(Qtable):
    state, _ = env.reset()
    path = [state]
    done = False
    while not done:
        action = np.argmax(Qtable[state])
        new_state, reward, terminated, truncated, info = env.step(action)
        done = terminated or truncated
        path.append(new_state)
        state = new_state
    return path

# 训练参数
n_training_episodes = 10000  # 训练回合数
learning_rate = 0.7          # 学习率
gamma = 0.95                 # 折扣因子
max_steps = 99               # 每回合最大步数
max_epsilon = 1.0            # 初始探索概率
min_epsilon = 0.05           # 最小探索概率
decay_rate = 0.0005          # 探索概率衰减率

# 初始化环境
env = gym.make('FrozenLake-v1', is_slippery=False)

# 训练过程
for episode in range(n_training_episodes):
    state, _ = env.reset()  # 初始状态
    step = 0
    done = False
    epsilon = min_epsilon + (max_epsilon - min_epsilon) * np.exp(-decay_rate * episode)

    while not done and step < max_steps:
        action = epsilon_greedy_policy(Qtable, state, epsilon)
        new_state, reward, terminated, truncated, info = env.step(action)
        done = terminated or truncated
        # Q值更新公式
        Qtable[state, action] = Qtable[state, action] + learning_rate * (reward + gamma * np.max(Qtable[new_state]) - Qtable[state, action])
        state = new_state
        step += 1

n_eval_episodes = 100
mean_reward = evaluate_agent(Qtable, n_eval_episodes)
print(f"{n_eval_episodes}个回合的平均奖励: {mean_reward:.2f}")

path = visualize_path(Qtable)
print("智能体走过的路径:", path)